Autocorrelation
Tempo Estimation
The beat (or pulse) of a musical piece is a periodic sequence of events or impulses. By examining the periodic structure of the impluses, we can try to estimate what one period is (the distance of a beat), which will allow us to guess the tempo.
Autocorrelation
We have learned about correlation. Autocorrelation is used to find how similar a signal, or function, is *to itself* at a certain time difference, which is referred to as lag.
For example, let's say I have the following sequence:
vals = np.array([4,1,3,1,4,1.5,2.5,0.2,3.5,1,2,1.5])
Let's make a plot to see it better:
plt.stem(vals, use_line_collection=True)
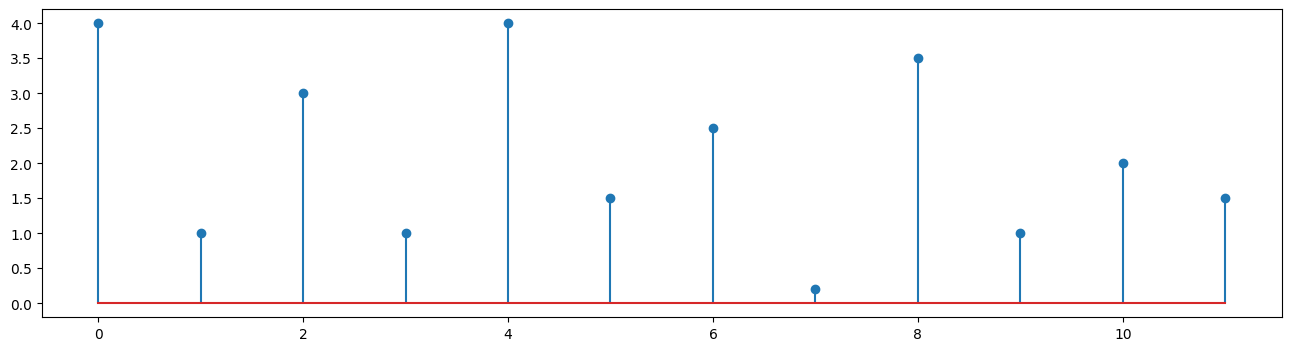
An autocorrelation will compare this original array to every possible shifted version of itself.
a = np.roll(vals, -1)
b = np.roll(vals, -2)
c = np.roll(vals, -4)
plt.stem(vals, use_line_collection=True)
(markers, stemlines, baseline) = plt.stem(b, use_line_collection=True)
plt.setp(markers, marker='D', markersize=10, markeredgecolor="orange", markeredgewidth=2)
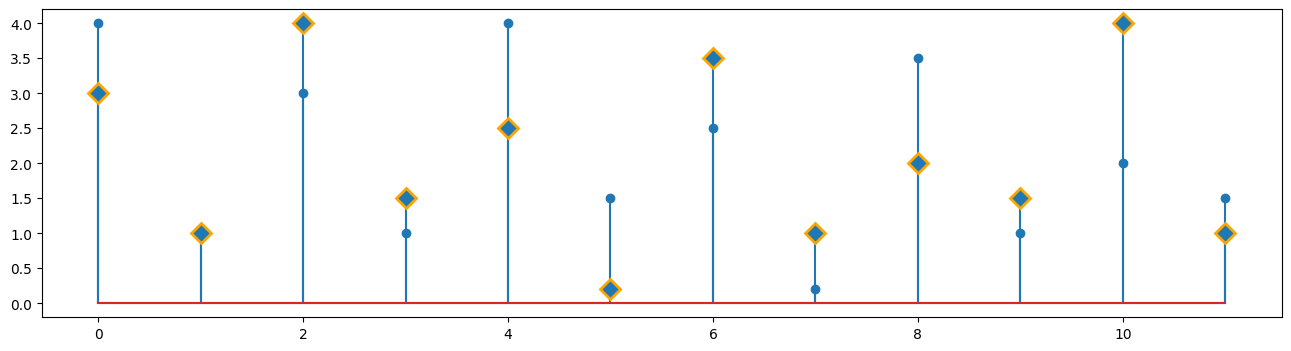
np.corrcoef(vals, c)
array([[1. , 0.8598234],
[0.8598234, 1. ]])
Test it out on Energy values
(fs, x) = read('../audio/80sPopDrums.wav')
xnorm = x/np.abs(x.max())
time = np.arange(0,xnorm.size/fs,1/fs)
hop_length = 512 # 50% overlap
frame_length = 1024
energy = feature.rms(xnorm, hop_length=hop_length, frame_length=frame_length)
len(energy[0])
752
frames = range(len(energy[0]))
t = frames_to_time(frames, sr=fs, hop_length=hop_length)
t.shape
(752,)
import matplotlib.pyplot as plt
plt.figure(figsize=(15,4))
plt.plot(time, xnorm, alpha=0.3)
plt.plot(t, energy[0], 'g--');
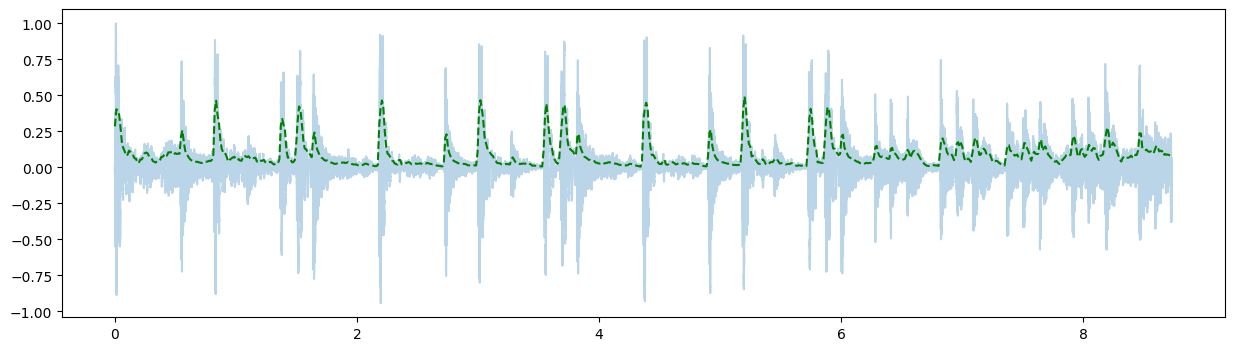
diff = energy[0][1:] - energy[0][0:-1]
#half-wave rectification - use numpy.where to set elements of array when condition is satisfied
diff = np.where(diff < 0, 0, diff)
#diff[diff < 0 ] = 0
plt.figure(figsize=(15,4))
plt.plot(t[1:], diff)
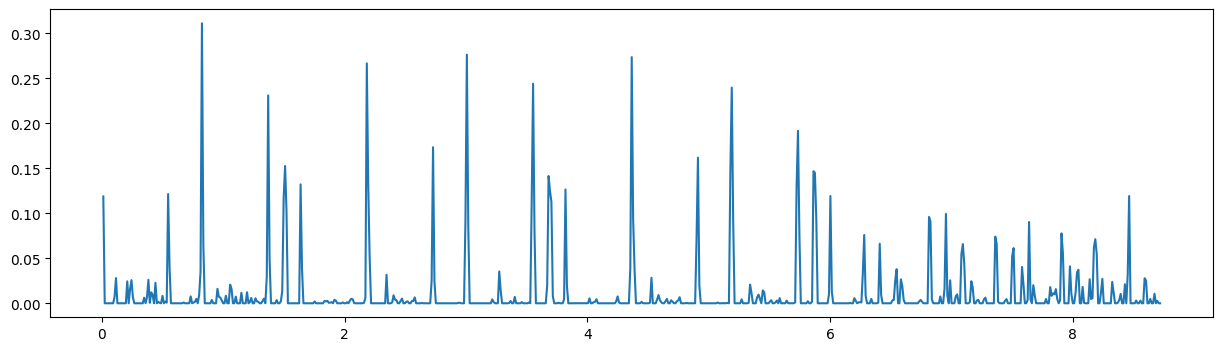
xplines = diff > 0.03
xplines[:20]
array([ True, False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False, False,
False, False])
plt.figure(figsize=(15,4))
plt.plot(time, xnorm, alpha=0.3)
plt.plot(t, energy[0], 'g--');
for xc in t[1:][xplines]:
plt.axvline(x=xc, linestyle='--')
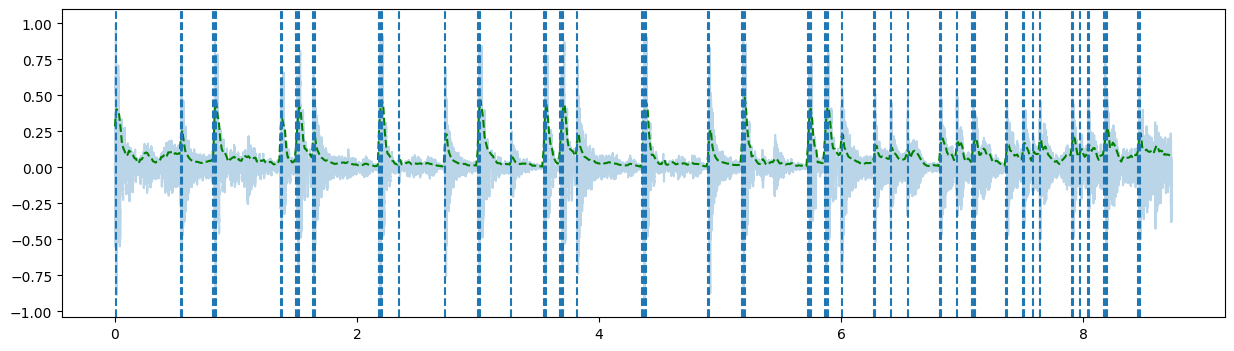
We can use librosa.clicks to check how we are doing (click to see detail)
import librosa
clicks = librosa.clicks(times=t[1:][xplines], sr=fs, hop_length=None)
print(xnorm.size, clicks.size)
384993 377658
clicks.resize(xnorm.shape)
combn = clicks + xnorm
from IPython.display import Audio
Audio(combn, rate=fs)
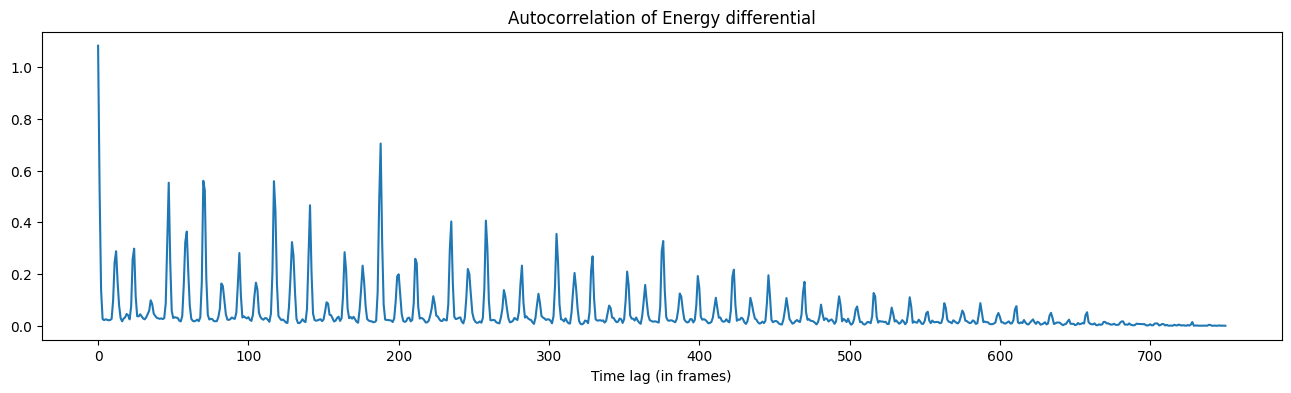
ac = librosa.autocorrelate(diff)
plt.plot(ac)
plt.title('Autocorrelation of Energy differential')
plt.xlabel('Time lag (in frames)')
ac.max()
1.0824595377261215
ac[0]
1.0824595377261215
v = ac[1:].max()
v
0.7043166239738892
points = np.where(ac > 0.4) #ignore zero and one
points
(array([ 0, 1, 47, 70, 71, 117, 118, 141, 187, 188, 235, 258]),)
Calculate the times between successive spikes (each frame increments by 512 samples).
fsec = 512/fs
fsec
0.011609977324263039
points = np.array(points)
t_inc = fsec * points
# ignore first two values (zero and one)
t_inc[0][2:]
array([0.54566893, 0.81269841, 0.82430839, 1.35836735, 1.36997732,
1.6370068 , 2.17106576, 2.18267574, 2.72834467, 2.99537415])
#calculate the differences between the values
ts = t_inc[0][2:]
ts[1:] - ts[:-1]
array([0.26702948, 0.01160998, 0.53405896, 0.01160998, 0.26702948,
0.53405896, 0.01160998, 0.54566893, 0.26702948])
Notice that .011, .276, and .534 (approximately) recur (in seconds). 60 divided by these values gets us estimated tempo.
tempa = 60 / .011
tempb = 60 / .267
tempc = 60 / .534
print( tempa, tempb, tempc)
5454.545454545455 224.7191011235955 112.35955056179775
Given the "normal" range of tempi, tempc is the most likely. Check with tempo calculator.